Decibeli õpetus: dB ja dBm vs Gain ja Milliwatts

Detsibeli (dB) mõiste on arusaadavalt keeruline ja segane kellelegi, kellele seda lihtsalt tutvustatakse. Võimenduse, võimsuse ja pinge (ja voolu, kuid mitte nii sageli) spetsifikatsioonide ühendamine, mis segavad dB, dBm, dBW, vatti, millivatti, pinget, millivolti jne, nõuab sageli lineaarväärtuste ja detsibellide väärtuste vaheliseks muundamist edasi-tagasi. See lühike õpetus aitab selgitada erinevust detsibellidega töötamise ja lineaarsete väärtustega töötamise vahel.

Logaritmid (logid) kujutasid šoti matemaatik John Napier esmakordselt välja 1600-i alguses kui vahendit korrutamis- ja jagamistoimingute lihtsustamiseks, muutes need vastavalt kiiremaks ja vähem veaohtlikuks liitmis- ja lahutamistoiminguks. See on võimalik tänu sellele, et eksponentidega sarnaste põhinumbritena väljendatud kahe arvu korrutamine on võimalik eksponentide lihtsalt liitmise teel. Nende samade numbrite jagamine toimub eksponentide lahutamise teel. See on üks eksponentide seadusi ja näeb välja selline:

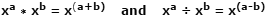
Kasutades näitena tegelikke numbreid, kus x = 10, a = 4, b = 1:

Eksponentide seadus töötab mis tahes põhinumbri, mitte ainult 10i puhul. Mõistmiseks:

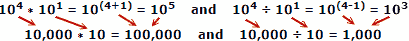
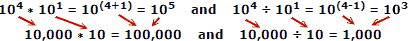
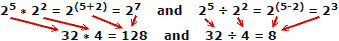
Inimesed teevad numbrite liitmisel ja lahutamisel vähem vigu, seega on logaritmide eelis ilmne. Pidage meeles, et logaritmid töötati välja enne, kui mehaanilised või elektroonilised arvutid olid saadaval. Slaidireegel kasutab arvutamiseks välja logaritmide omadusi, kuid see on eraldi põhiteema.

Need on lihtsad näited, kuid kehtivad iga aluse või eksponendi kohta. Kalkulaatori puudumisel on üldiseks kasutamiseks kasulik arvandmete tabel ja nende ekvivalentsed logaritmid. Varased logitabelid täitsid mahtusid, sõltuvalt numbrite vahekaugusest (1.000, 1.001, 1.002, 1.003, vs. 1.0, 1.1, 1.2, 1.3 jne). Hea uudis logaritmitabelite loojatele on see, et vaja on ainult ühte numbrikümnendikku (nt 1 kuni 10), kuna iga eelnev või sellele järgnev kümnend on 10i võimsuse lihtne kordne.

Märkus. Ma kasutan selles arutelus alust 10, kuna see on meie ühise numbrite süsteemi alus - sellest tulenevalt kasutatakse terminit „ühine logaritm” 10-i põhilogide jaoks. Võib-olla olete kuulnud naturaalsetest logaritmidest, mis kasutavad e alust, kuid skalaarse elektrienergia, pinge ja voolukoguste arvutamisel ei kasutata e sageli (kuigi seda kasutatakse faasinurkade, st Euleri identiteedi arvestamisel). Naturaalsed logaritmid kirjutatakse ln (x) -na ilma e-alaindeksita, samas kui 10-i baaslogaritmid kirjutatakse lihtsalt logina (x) ilma 10-i alaindeksita; st mitte vastavalt loge (x) või log10 (x).

Aluse kohta = 10 logitabel:

Poollogaritmiline 5 tsüklite tehniline graafikapaber - RF CafeErand ja erijuhtum on logx (0) = määratlemata. Seda seetõttu, et pole voolu, millele saaksite arvu tõsta ja saada 0 (null). Võite asümptootiliselt nullile läheneda, kuid nulli ei pääse. Logiskaalal ei kuvata kunagi numbrit nulli; tavaliselt töötavad nad 10i võimsusest mõne muu võimsuseni kümme. Paremal on näidatud logigraafikapaberi näide. Selle vahemik on 5 'tsüklit' või 'aastakümmet'. Pange tähele, et y-teljel pole nulli.

Arvu baas-10 (tavaline) logaritm on eksponent, milleni 10 tuleb tõsta, et saada see arv. Teisisõnu, kuna 10, mis on tõstetud 2 võimsusele, võrdub 100 (102 = 100), on 10i base-100 log 2 (log10 100 = 2).

See on logaritmide põhiseadus:


Tehakse samad korrutused ja jagamised, mis lehe ülaosas, kasutades tegelikke logaritme:



See sobib, kuid lõpuks jõuate otsitava numbri logaritmini. Küsimus: Kuidas saada vajalikku vastust, välja arvatud selline lihtne näide nagu see? Vastus: otsige tulemuse antilogaritmi (antilog). Sel juhul:

Karmim ja tõenäolisem näide numbritega, mis ei ole 10 täisarvud, võib välja näha järgmine:




 HP-35 kalkulaator (wikipedia) - RF CafeKuna logaritm 'x' võrdub 1.8444, antilog võrdub 'x', mis on 69.9



Kasutasin nende numbrite logide ja antilogide otsimiseks oma kalkulaatorit, kuid enne 1972-i, kui Hewlett Packard (HP) tutvustas oma teaduslikku kalkulaatorit HP-35, oli keskmine inimene, kellel ei olnud juurdepääsu logi kasutamiseks ettevõtte või ülikooli suurarvutitele. tabel selliste arvutuste tegemiseks.

Kes viitsib täna logaritme kasutada, võiksite küsida? Kasseeritud süsteemi parameetrite, näiteks mürataseme (NF) ja pealtkuulamispunktide (IP) arvutamisel on palju inimesi, kaasa arvatud mina. Võimsuse dB ja võimsuse dBm väärtuste lihtne liitmine ja lahutamine NF ja IP korral ei tööta. Reguleerivad valemid kasutavad lineaarse võimenduse ja võimsuse väärtuste korrutamist ja jagamist, mis nõuab kõigepealt dB ja / või dBm teisendamist antigloogide abil lineaarseteks arvudeks (võimendussuhe ja mW), kaskaadarvutuste tegemist ja seejärel tulemuse teisendamist tagasi dB ja / või dBm logide abil.

Kõik süsteemi kaskaaditoimingud ei vaja edasi-tagasi teisendamist. Näiteks kui on vaja ainult kogu süsteemi võimendust ja / või väljundvõimsuse taset, võib arvutused teha kas lineaarsete ühikutega (mW ja kordajad) või logaritmiliste ühikutega (vastavalt dBm ja dB).

„DB” ja „dBm” määratlus

Detsibell (dB) elektrotehnikas määratletakse kui 10 korda baas-10 logaritm korda kahe võimsustaseme vahel; nt Pout / Pin (teisisõnu võimendus). Mõistmiseks:

Kõik kasumid, mis on suuremad kui 1, väljendatakse seetõttu positiivsete detsibellidena (> 0) ja väiksemad kui 1 kasumid väljendatakse negatiivsete detsibellidena (<0). Pange tähele, et juhtudel, kus enamik meist kohtab, peab P1 / P2 lineaarne suhe olema positiivne arv (> 0), kuna 0 logaritm on määratlemata ja negatiivsete arvude logaritm on keeruline (need sisaldavad nii reaalset kui ka kujuteldavat osa ). Kuid dB väärtus võib teoreetiliselt omandada mis tahes väärtuse vahemikus −∞ kuni + ∞, sealhulgas 0, mis on võimendus 1 [10 * log (1) = 0 dB].

'dBm' on detsibellidel põhinev jõuühik, millele viidatakse 1 mW. Kuna 0 dB võimendus on võrdne 1 võimendusega, on 1 mW võimsus 0 dB suurem kui 1 mW või 0 dBm. Samamoodi on dBW võimsuse ühik detsibellides võimsuse 1 W suhtes.


Järelikult on kõik dBm väärtused, mis on suuremad kui 0, suuremad kui 1 mW, ja kõik dBm väärtused, mis on väiksemad kui 0, on väiksemad kui 1 mW (vt joonis 1). Näiteks + 3.01 dBm on 3.01 dB suurem kui 1 mW; st või 0 dBm + 3.01 dB = + 3.01 dBm (2 mW). −3.01 dBm on 3.01 dB väiksem kui 1 mW; st või 0 dBm + (−3.01) dB = −3.01 dBm (0.5 mW).

Järgmises tabelis on toodud arvulised näited, et saaksite näha korrelatsiooni mW ja dBm vahel. Sama logaritmilisel skaalal esitatud väärtuste komplekt annaks sirgjoone. Logaritmilise seose tõttu koondab graafik väiksemat väärtust vasaku vertikaaltelje suhtes. Piirkonna 0 kuni 1 mW suurendusega versioon on selguse huvides sisestatud.

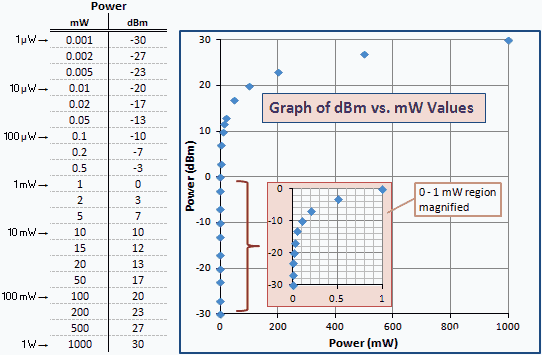
Joonis 1 - võimsuse graafik ühikutes dBm vs mW

Joonis 2 on tabel ja graafik dB vs lineaarsete võimendussuhete kohta, mis on sarnased dBm vs mW joonisel 1. Pange tähele, et numbrid ja kõverad on täpselt samad; ainult telje sildid on muudetud. Selle põhjuseks on asjaolu, et dBm on võimsuse ühik, mida väljendatakse dB 1 mW (0 dBm) suhtes.

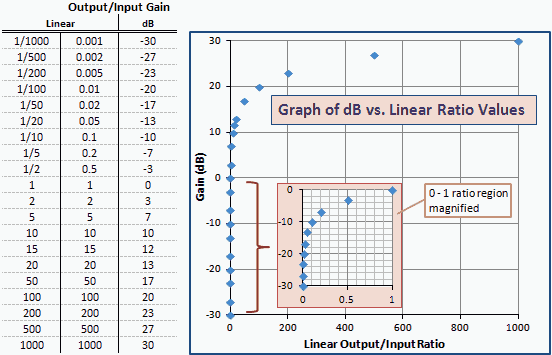
Joonis 2 - võimenduse graafik dBm ühikutes vs lineaarsuhet

Põhimõtteliselt on võimendus korrutustegur (või jaotus). Näiteks võib võimendil olla võimendus, mis suurendab signaali sisendist väljundini 4 (st 4x) võrra (vt joonis 3). Kui võimendisse suunatakse 1 mW (0 dBm) signaal, väljub 1 mW * 4 = 4 mW. Detsibellides võrdub 4-i tegur 10 * log (4) = 6.02 dB-ga, seega 0 dBm pluss 6.02 dB võimenduse saagisega + 6.02 dBm väljundis.

1 mW * 4 = 4 mW

0 dBm + 6.02 dB = 6.02 dBm

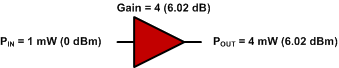
Joonis 3 - ühe võimendi võimendus.

Kasumi (lineaarse ja dB) kombineerimine positiivse väärtusega

Kui võimendi võimendusega 4 on jadas teise võimendiga, mille võimendus on 6, siis on koguvõimendus 4 * 6 = 24. Detsibellides on 6 tegur võrdne 10 * log (6) = 7.78 dB ja 24 tegur on samaväärne 10 * log (24) = 13.8 dB.

Nii nagu 4 x 6 = 24 (lineaarne võimendus), 6.02 dB + 7.78 dB = 13.8 dB (detsibelli võimendus).

Kui võimendisse juhitakse 1 mW signaal (0 dBm), väljub 4 mW esimesest võimendist ja 24 mW teisest võimendist. Vt joonist 4.

1 mW * 4 * 6 = 24 mW
0 dBm + 6.02 dB + 7.78 dB = 13.8 dBm

Joonis 4 - kaskaadne kahekordse võimendi võimendus.

Kasumi ja kahjumi ühendamine (lineaarne ja dB)
See järgmine näide näitab, mis juhtub, kui tekib võimendus <1 (kaotus), kus esimese võimendi järel asetatakse 1/6 võimendusega summutaja teise võimendi asemel. Vt joonis 5.
4 * 1 / 6 = 2 / 3 (lineaarne võimendus). Samamoodi 6.02 dB - 7.78 dB = −1.76 dB (detsibelli võimendus).
Nagu eelmises näites, kui 1 mW signaal (0 dBm) juhitakse võimendisse 4 võimendusega, väljub 4 mW. See 4 mW läheb seejärel summutisse lineaarse võimendusega 1 / 6 ja väljub võimsuse tasemel 4 / 6 mW (2 / 3 mW).
Koguvõimendus on sel juhul 4 / 6 = 2 / 3, nii et väljundvõimsus on tegelikult väiksem kui sisendvõimsus.

1 mW * 4 * 1 / 6 = 2 / 3 mW = 0.67 mW

0 dBm + 6.02 dB + (-7.78 dB) = −1.76 dBm

Joonis 5 - kaskaadvõimendi võimendus ja summuti.

12 mW + 34 mW + 8 mW + 20 dB

Täiendav teave logaritmide kohta
Toodete logaritmid
Ülaltoodud kaudselt kasutatud logaritmide omadus on järgmine ja see on aluseks logaritmi väärtuste liitmiseks ja lahutamiseks nende lineaarsete ekvivalentide korrutamise asemel.

'h * j / k * m / n' võib tähendada komponentide kaskaadi, millel on kolm seadet (h, j ja m), kummagi võimendus> 1 ja kaks seadet (k ja n), igaüks võimendusega <1 (vt Joonis 6). Kogu süsteemi võimenduse saab arvutada, korrutades kõik lineaarse võimenduse väärtused kokku või liites kõik detsibellide võimenduse väärtused.

Joonis 6 - kaskaadkomponendid

Eksponentide logaritmid
Järgnev on oluline mõistmaks, miks võimsuse suurenemine võimsuse osas on 10 * log (Pout / Pin) dB, samal ajal kui võimsuse suurenemine pinge osas on 20 * log (Vout / Vin) dB.


mis tuleneb sellest, et cf on võrdne c-ga, korrutatuna iseenda f-korda. Näiteks kui f = 4:


Võimsuse suurenemine võimsuse alusel vs võimsuse suurenemine pinge alusel
Võimsuse suurendamine on Pout / Pin ja pinge võimendus on Vout / Vin. Võimsuse suurenemine, mis põhineb võimsuse suhtel detsibellides, on määratletud kui 10 * log (Pout / Pin). Võimsuse suurenemine pingena on [(Vout2 / R) / (Vin2 / R)], kuna Ohmi seaduse kohaselt on P = V2 / R. Nimetajates olev R tühistab Vout2 / Vin2 jätmise, mis on võrdne (Vout / Vin) 2-ga, nagu on määratletud eksponentide reegliga, mis ütleb ac / bc = (a / b) c. Seega:

Tähtis märkus: Pinge suurenemine pinge osas on 10 * log (Vout / Vin) dB, sama mis võimu suurendamisel võimsuse osas. 20 * log (Vout / Vin) dB võrrand kehtib ainult siis, kui võimsuse suurenemist väljendatakse pinges. See on tavaline segaduspunkt.


Ükski matemaatikaoperatsioon pole meelevaldne ja see kehtib ka selle kohta, miks signaali võimsuse kadu (võimendus <1) kujutatakse negatiivse väärtusena ja lahutatakse seega kaskaadi arvutamisel. See on lihtne demonstratsioon, kuid väärib märkimist.

log (1 / f) = log (1) - log (f) = 0 - log (f) = -log (f)

Kui soovite raadiojaama ehitada, täiustage oma FM-raadiosaatjat või vajate mõnda muud FM-seadmed, palun võtke meiega ühendust: [meiliga kaitstud].

Jäta sõnum 

Sõnumite nimekiri