tooted Kategooria
- FM-saatja
- 0-50w 50w-1000w 2kw-10kw 10kw +
- TV-saatja
- 0-50w 50-1kw 2kw-10kw
- FM antenn
- TV Antenna
- antenn Accessory
- Kaabel Connector Võimsus Splitter dummy Load
- RF Transistor
- Laboratooriumi toiteallikas
- Audio seadmed
- DTV Front End seadmed
- link süsteem
- STL süsteemi Mikrolaineahi Link süsteemi
- FM-raadio
- power Meter
- Muud tooted
- Spetsiaalne koroonaviiruse jaoks
tooted Sildid
Fmuser saidid
- es.fmuser.net
- it.fmuser.net
- fr.fmuser.net
- de.fmuser.net
- af.fmuser.net -> afrikaans
- sq.fmuser.net -> albaania keel
- ar.fmuser.net -> araabia
- hy.fmuser.net -> Armeenia
- az.fmuser.net -> aserbaidžaanlane
- eu.fmuser.net -> baski keel
- be.fmuser.net -> valgevenelane
- bg.fmuser.net -> Bulgaaria
- ca.fmuser.net -> katalaani keel
- zh-CN.fmuser.net -> hiina (lihtsustatud)
- zh-TW.fmuser.net -> Hiina (traditsiooniline)
- hr.fmuser.net -> horvaadi keel
- cs.fmuser.net -> tšehhi
- da.fmuser.net -> taani keel
- nl.fmuser.net -> Hollandi
- et.fmuser.net -> eesti keel
- tl.fmuser.net -> filipiinlane
- fi.fmuser.net -> soome keel
- fr.fmuser.net -> Prantsusmaa
- gl.fmuser.net -> galicia keel
- ka.fmuser.net -> gruusia keel
- de.fmuser.net -> saksa keel
- el.fmuser.net -> Kreeka
- ht.fmuser.net -> Haiti kreool
- iw.fmuser.net -> heebrea
- hi.fmuser.net -> hindi
- hu.fmuser.net -> Ungari
- is.fmuser.net -> islandi keel
- id.fmuser.net -> indoneesia keel
- ga.fmuser.net -> iiri keel
- it.fmuser.net -> Itaalia
- ja.fmuser.net -> jaapani keel
- ko.fmuser.net -> korea
- lv.fmuser.net -> läti keel
- lt.fmuser.net -> Leedu
- mk.fmuser.net -> makedoonia
- ms.fmuser.net -> malai
- mt.fmuser.net -> malta keel
- no.fmuser.net -> Norra
- fa.fmuser.net -> pärsia keel
- pl.fmuser.net -> poola keel
- pt.fmuser.net -> portugali keel
- ro.fmuser.net -> Rumeenia
- ru.fmuser.net -> vene keel
- sr.fmuser.net -> serbia
- sk.fmuser.net -> slovaki keel
- sl.fmuser.net -> Sloveenia
- es.fmuser.net -> hispaania keel
- sw.fmuser.net -> suahiili keel
- sv.fmuser.net -> rootsi keel
- th.fmuser.net -> Tai
- tr.fmuser.net -> türgi keel
- uk.fmuser.net -> ukrainlane
- ur.fmuser.net -> urdu
- vi.fmuser.net -> Vietnam
- cy.fmuser.net -> kõmri keel
- yi.fmuser.net -> Jidiši
Võimsus ja amplituud: vattides, voltides ja viidatud detsibellides
Sissejuhatus
Raadiosagedusrakendustes (aga ka paljudes muudes rakendustes) on väga levinud väga suurte ja väga väikeste signaalide käsitlemine. Näiteks võib transiiver edastada 100 W võimsust ja võtta vastu ainult 10 fW (või 0.000'000'000'000'01 W). Nendel äärmiselt erinevatel võimsustasemetel võivad olla samad vooluahelad. Muidugi saab neid arvnäitajaid väljendada vattides, kasutades tehnilist märget (nagu ülalpool) või teaduslike märkustega, näiteks 1 · 102 W ja 1 · 10 – 14 W, kuid neid on üsna raske hääldada ja kui eksponent on valesti kirjutatud , on sellest tulenev viga tohutu.
Teine võimalus on võtta logaritm ja teisendada kõik jõud dBm-des. 100 W muutub + 50 dBm ja 10 fW muutub –110 dBm: neid arvnäitajaid on südamega käsitseda ja kirjutada palju lihtsam. Siis, kui ka erinevate vooluringiplokkide sumbumine ja võimendus on väljendatud ka dB-des, saab lõpliku võimsuse leidmiseks korrutamise asemel kõik lihtsalt kokku liita, arvutusi veelgi lihtsustades.
Kõigile ei meeldi dB, dBm ja sarnased (pseudo) moodulid: nende kasutamiseks pole ranget vajadust, kuid neid kasutatakse tehnika valdkonnas nii laialdaselt, et neid on väga keeruline vältida.
Mingi teooria
Detsibellides (dB) kasutatakse võimsussuhete väljendamiseks logaritmilisel viisil, nii et väga suuri ja väga väikeseid võimsusi saab võrrelda mugavate arvude abil. Detsibell on mõõtmeteta pseudoühik, kuna seda määratletakse kahe jõu suhtega. Kuid kuna detsibellid on mõõtmeteta suhte asemel tõelise võimsuse väljendamiseks nii käepärased, kasutatakse väga sageli viidatud detsibelle.
Kui räägime võimsusest, määratleb järgmine võrrand võimsuse p0-i võimsustaseme P (dB) võimsuses p W (W):
10 tegur on tingitud asjaolust, et detsibellid on "Bellsist kümnes". Kuid ma pole kunagi kuulnud ühestki Bellsis tehtud mõõtmisest, kasutatakse ainult detsibelle.
Kõige tavalisem ühik on dBm (hääldatakse "dBm"), mida tuntakse ka kui dBmW või detsibell-millivatti: see on lihtsalt võimsuse tase dB-des, võrreldes etalonvõimsusega p0 = 1 mW. Mõnikord kasutatakse ka dBW ja need väljendavad võimsuse suhet p0 = 1 W suhtes, kuid need pole eriti levinud.
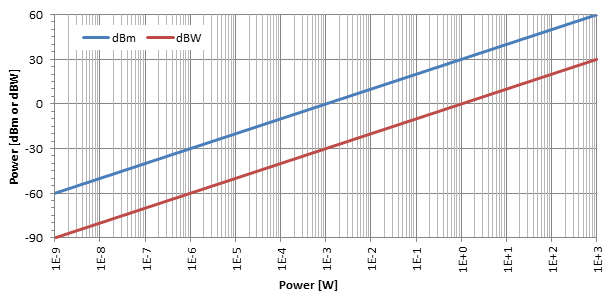
Nagu ülaltoodud graafikul näidatud, on detsibellide muundamise logaritmiline efekt üsna ilmne. Nagu sellel logiliini graafikul näha on, on dBm ja dBW lihtsalt kaks sirget, mida eraldab 30 dB: dBm teisendamiseks dBW lahutatakse lihtsalt 30.
Mõnes valdkonnas, nagu analoogtelevisiooni vastuvõtt, on tavaline, et mõõdetakse pinge, mitte toide. See pole probleem, kui takistus on teada ja fikseeritud (televiisorid kasutavad tavaliselt 75 Ω).
Absoluutpingetel on võimalik kasutada ära ka detsibellide logaritmilist skaalat, kasutades detsibell-mikrovolti (dBμV) ja detsibell-volti (dBV). Kõige tavalisem on dBμV, mis väljendavad pingesuhet u0 = 1 μV suhtes. Mõnikord kasutatakse ka dBV ja need väljendavad pinge suhet u0 = 1 V suhtes.
Hoiduge sellest, et pinged kasutavad dB valemis "20" asemel "10". Selle põhjuseks on asjaolu, et detsibellid on alati määratletud kui jõuarv; kui meil on ainult pinged, peame need jõudluse leidmiseks kõigepealt ruudus jagama. See kahe võimsus logaritmist välja võttes korrutab olemasoleva 10 teguri 2-iga.
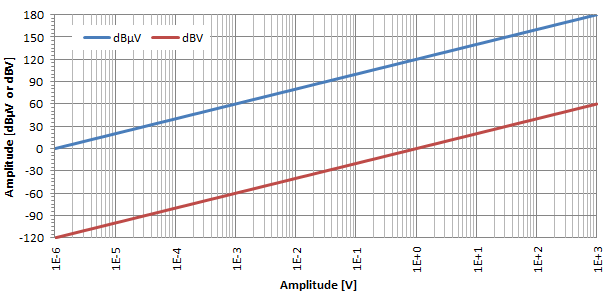
Nagu ülaltoodud graafikul näidatud ja sarnasel viisil nagu varem, on detsibellide muundamise logaritmiline efekt üsna ilmne ka pingete puhul. Nagu sellel logiliini graafikul näha on, on dBμV ja dBV lihtsalt kaks sirget, mida eraldab 120 dB: dBμV teisendamiseks dBV-ks lahutatakse 120 lihtsalt.
Kui tahame muundada toitepingeks ja vastupidi, peame teadma impedantsi. Me kasutame lihtsalt järgmist võrrandit:
See teisendus kehtib ainult siis, kui takistus Zc on reaalne ja koormus on sobitatud ülekandeliiniga.
Kui joonestame võimsustaseme dBm-s ja amplituuditaseme dBμV-s võimsuse funktsioonina W-dena antud impedantsi korral (siin Zc = 50 Ω), saame järgmise:
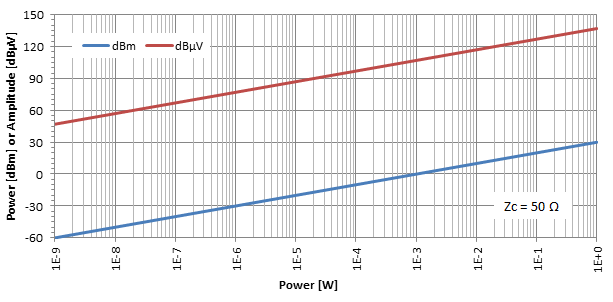
Praktilised kaalutlused
Esmapilgul võib arvata, et logaritmi tõttu on dBm-iga tegelemiseks hädavajalik taskuarvuti. Tegelikult saab umbmäärase arvutuse teie peas hõlpsasti teha. Peate meeles pidama vaid kolme fakti:
Võimsus 1 mW on 0 dBm.
Iga kord, kui võimsus kahekordistub, lisage 3 dB.
Iga kord, kui võimsus suureneb 10 korda, lisage 10 dB.
Vaatleme nüüd mõnda näidet: oletame, et meil on võimsuse tase 26 dBm. Võime kirjutada 26 dBm = 0 dBm + 10 dB + 10 dB + 3 dB + 3 dB ja eelneva kolme lihtsa reegli abil saame võimsuse hõlpsalt leida, tehes 1 mW · 10 · 10 · 2 · 2 = 400 = XNUMX .
Teine näide: Oletame, et meil on -33dBm: saame kirjutada kui -33 dBm = 0 dBm - 10 dB - 10 dB - 10dB - 3 dB ja me leiame 1 mW / 10 / 10 / 10 / 2 = 0.5 mikrolainetega.
See toimib ka teisiti, näiteks 50 mW on lihtsalt 1 mW · 10 · 10 / 2. DBm-des on meil 0 dBm + 10 dB + 10 dB –3 dB = 17 dBm.
See nõuab teatavat harjutamist, kuid seda on väga lihtne teha. See pole nii täpne kui taskuarvuti, kuna saate olla täpsed ainult ± 2 dB juures, kuid annab pingutuse huvides signaali tugevusest väga hea ettekujutuse.
Sarnane meetod töötab ka dBμV korral, kuid reeglid on erinevad:
1 μV amplituud on 0 dBμV.
Iga kord, kui amplituud kahekordistub, lisage 6 dB.
Iga kord, kui amplituud suureneb 10 korda, lisage 20 dB.
Võite olla üllatunud eelnevalt näidatud arvutustes detsibellides, kus dB-le lisatakse dB, mis on üsna kummaline. Seda seetõttu, et detsibellid on pseudoühikud ja ei käitu nagu tavaliselt. Kahe võimsuse suhe on väljendatud dB, kuid on mõõtmeteta: näiteks 3 dB tähendab ainult "kaks korda rohkem". DBm-s väljendatud võimsus on tõesti võimsus: näiteks 10 dBm tähendab "10 korda tugevam kui 1 mW", mis on 10 mW.
Kui lisate detsibellid (dB, dBm, ...), korrutate nende logaritmilise olemuse tõttu tegelikult algsed arvud. Niisiis, kui lisate 3 dB võimendusele 10 dBm, saate 13 dBm. Kuid mida sa tegelikult tegid, korrutades teguri 2 võimsusega 10 mW, saate 20 mW, mis on 13 dBm!
Siiani on nii hea, et lisamist on peas palju lihtsam teha kui korrutamist ning see teeb detsibellidest nii käepärase. Kuid on probleem: kuna detsibellide liitmine vastab algtegurite korrutamisele, kuidas saab kahe signaali võimsust lisada (kombineerida)? No ei saa. DBm-i ei saa lisada. Kui teil on näiteks vooluahel või seade, mis ühendab ühe signaali võimsuse 10 dBm (10 mW) teise signaali võimsusega 13 dBm (20 mW), on tulemuseks 10 mW + 20 mW = 30 mW, mis on 14.8 dBm. Otseselt dBm-is seda teha ei saa, peate mõlemad jõud Wattsis teisendama, liitma ja dBm-ga tagasi teisendama. See on detsibellide suur piirang ja ühine lõks; Õnneks pole see operatsioon eriti tavaline.
Kui soovite raadiojaama ehitada, täiustage oma FM-raadiosaatjat või vajate mõnda muud FM-seadmed, palun võtke meiega ühendust: [meiliga kaitstud].

